
М. Алтайский, к.ф.-м.н.
Считается, что основы современной математики - ее геометрической части - были заложены в работах Евклида, а дифференциального исчисления - основы современного математического анализа - в трудах Ньютона и Лейбница. Имеется, однако, ряд работ, неизвестных широкому кругу читателей, в которых рассматриваются элементы математического знания, изложенные в Ведах - древнейшем памятнике человеческой культуры, превосходящем по возрасту, по крайней мере, на несколько тысяч лет все известные древнегреческие труды. Веды, в переводе с санскрита источник знания (ср. с русск. ведать), согласно индийским верованиям, содержат все знания, как научные, так и этические, исходно данные человечеству. Веды, написанные на санскрите в форме коротких изречений (сутр), не содержат теорем и математических выкладок. Вместо этого имеются операционные инструкции - правила решения определенных задач. Интерпретация инструкций требует как глубокого знания ведической культуры, так и профессиональной математической подготовки. Адаптировал математическое содержание ведического знания выдающийся индийский мыслитель Шанкарачарья Шри Барати Кришна Тиртха (1884-1960). Глубоко изучив ведическое знание, он планировал написать 16 томов ведической математики, включающие арифметику, алгебру, геометрию, тригонометрию, теорию конических сечений, астрономические вычисления, дифференциальное и интегральное исчисление. К сожалению, при жизни он успел подготовить только первые два тома, в которые вошли элементы арифметики, алгебры полиномов и геометрии. Ведическая математика в изложении Шри Шанкарачарья, хотя и сводится к хорошо известным западному читателю теоремам, содержит настолько удобные способы их приложения, что часто представляется практически чудом. Так, мгновенное умножение в уме семизначных чисел оказывается возможным с помощью хорошо известных свойств алгебры полиномов. Выступления Шанкарачарья с лекциями по ведической математике с восторгом встречались в университетах США и Индии. Предлагаем вашему вниманию выборочное изложение "Ведической математики" Шри Барати Кришны Тиртха, выдержавшей несколько английских изданий, но неизвестной российскому читателю.
Попробуем умножить 98х99 обычным способом, в столбик:

Объем этой процедуры невелик, а сам процесс не столь утомителен, если
умножаются двузначные числа. Трудности, однако, стремительно возрастают
с увеличением числа значащих цифр. Что же обозначает знак х
? Оба числа в рассматриваемом примере незначительно отличаются от 100,
умножение же
100 х100 = 10 000 не вызывает затруднений. Это наводит на мысль
применить тождество
(x - a) (x - b) = x (x - a - b) + ab, x = 100, a = 2, b = 1. Здесь и оправдывается
правило х ("крест накрест"). Рассмотрим еще один пример. Умножим
98 на 99 по правилу "крест накрест". Имеем:

Основанием является число x = 100, соответствующие дополнения a = 2 = 100 - 98, b = 1 = 100 - 99. Разности x - a - b стоят крест накрест. Естественно, 98 - 1 = 99 - 2, поскольку x - a - b = x - b - a. Отсюда следует практическое правило (см. пример): выбрав основание (в данном случае x = 100, 2 разряда), записать недостатки справа от самих чисел со знаком минус (если сомножитель превосходит выбранное основание, то ставится плюс; так, 102 записывается в виде 100 + 02); затем поместить в первые два разряда результат разности крест накрест - (x - a - b) (в данном случае 100 - 2 - 1 = 98 - 1 = 99 - 2 = 97), а в последние два разряда поместить произведение дополнений (в данном случае a х b = 2 х 1 = 2). Для удобства вычислений первые два разряда отделяются от двух последних косой чертой.
Благодаря такому способу умножения, в древней Индии считалось необходимым знать на память таблицу умножения не 10 х 10, как принято в настоящее время у нас, а лишь 5 х 5: остальная часть таблицы может быть получена методом дополнений. Умножим, например, 6 на 7. Имеем

Здесь возникает необходимость использования косой черты между первым
и последними разрядами результата. Основание x = 10 в данном случае имеет
один разряд, однако произведение дополнений
ab = 3x4 = 12 содержит два разряда. Поэтому старший разряд произведения
дополнений пишется под косой чертой, а затем прибавляется к кросс-разности
3 + 1 = 4. С помощью этой операции нетрудно получить всю таблицу умножения.
Так
9-1 9-1 9-1 9-1 8-2 8-2 8-2 7-3 9-1 8-2 6-4 5-5 8-2 7-3 6-4 7-3 _______________________________ 8/1 7/2 5/4 4/5 6/4 5/6 4/8 4/9 |
Рассмотренный метод может быть применен, и в том случае, если основание не является целой степенью числа 10. Соответствующая сутра записывается так: "Anurupyena" (пропорционально). Отметим, что десятичные цифры, обычно называемые арабскими, в действительности являются санскритскими числительными.
1 2 3 4 5 6 7 8 9 10 эк до тин чар панч чё сат ат нё дас
Рассмотрим пример умножения "крест накрест" с использованием правила пропорциональности. Умножим 41 на 42:
41 - 09
42 - 08
_______
2) 33 / 72
16 /5 72
_______
17 / 22 |
Ближайшее "удобное" основание x = 50 = 100/2; фактор пропорциональности
2. Умножение, как и раньше, производится здесь по правилу (x - a) (x -
b) = x (x - a - b) + ab. Однако, поскольку первый член произведения
x (x - a - b) в схеме "крест накрест" технически учитывается лишь числом разрядов,
необходимо разделить второй член произведения на фактор пропорциональности.
В данном случае
x = 50, a = 9, b = 8, x - a - b = 33, = 16,5. Дробная часть числа 16,5,
т. е. 5 единиц младшего разряда, пишется под косой чертой, отделяющей старшие
разряды от младших. Затем выполняется еще одна операция сложения, указанная
на рисунке дополнительной горизонтальной линией. Если воспользоваться упоминавшейся
ранее алгебраической формулой, то нетрудно увидеть, что кросс-умножение
"работает" и в том случае, если хотя бы один из сомножителей превосходит
выбранное основание. В последнем случае необходимо обратить знаки сомножителей
a и b :
(x + a) (x + b) = (x + a + b) + ab.
Пример. 98 х 107 = 10486.

Здесь x = 100, a = - 2, b = + 7, x + a + b = 105, ab = - 14. Отрицательный знак произведения a x b ставится над младшими разрядами. так, -14 обозначается с чертой наверху. Знак произведения a x b здесь отрицателен, поэтому необходимо выполнить еще одну операцию сложения: 10500 + (- 14) = 10486. (Этой операции соответствует последняя строчка примера.) Аналогично умножаются и числа с большим числом разрядов. Умножим, например, два трехзначных числа: 635 х 504 = 320040.

Выбираем в качестве основания x = 500. Фактор пропорциональности 2 :
500 = 1000/2,
a x b = 135 x 4 = 540, кросс-сумма x + a + b = 639. Фактор пропорциональности,
как и ранее, записываем слева и отделяем круглой скобкой. Число 639 нечетное:
639/2= 319,5. Оставшиеся 5 единиц меньшего разряда записываем под косой
чертой 319/5 540 с последующим сложением.
Выше мы рассматривали простые примеры - умножение чисел, незначительно
отличающихся от "удобного" основания. Ведическая математика содержит также
общее правило умножения. Соответствующая сутра звучит так:
"rdhva Tiryaghyam"
- вертикально и крест накрест. Прежде чем перейти к конкретным примерам,
проиллюстрируем общую идею метода. Пусть необходимо умножить два числа
y и z. Запишем их в виде разложения по некоторому основанию a (чаще всего
a = 10):
y = ynan + yn-1an-1 + ... +
y1a1 + y0,
z = znan + zn-1an-1 + ... +
z1a1 + z0.
Их произведение таково: y x z = ynzn x a2n
+ (znyn-1 + ynzn-1)a2n-1
+
+ (ynzn-2 + yn-1zn-1 + yn-2zn)a2n-2 +
. . . . . . . .. . . . . . . . . . . . . +
+ (y2z0
+ y1z1 + y0z2)a2
+ (y1z0 + y0z1)a1
+ y0z0.
Первый и последний члены этого разложения отвечают чисто "вертикальным" произведениям, остальные - произведениям "крест на крест". Обозначая слагаемые в разложении y и z точками · и s соответственно, можно символически изобразить произведение y и z в следующем виде:

Здесь верхний ряд точек обозначает набор чисел (yn, yn-1, yn-2, ...), а нижний ряд треугольников - набор чисел (zn, zn-1, zn-2, ...). Умножение производится попарно, по соединительным линиям. Затем выполняется сложение всех произведений внутри каждой скобки. Приведем конкретные примеры. Пример 1.

Пример 2. .

в третьем разряде; при этом единица переносится в следующий (четвертый) разряд и пишется снизу. Аналогичная операция производится и в следующем примере.
Пример 3.

В заключение приведем пример умножения двух пятизначных чисел.
Пример 4.
87265 32117 __________ 2478727575 32396243 __________ 2802690005
Начнем рассмотрение с простейшего примера. Разделим 1 на 19 обычным способом - "в столбик":

Если нужно получить достаточно большое число значащих цифр, эта процедура становится утомительной: на каждом шаге требуется умножение соответствующей цифры частного на делитель с последующим вычитанием из остатка предыдущей операции. Благодаря вычислительной технике, в настоящее время нет необходимости выполнять такие вычисления; в древности же, например, при проведении астрономических расчетов, они были необходимы. Для быстрого и эффективного деления на числа, оканчивающиеся цифрой 9, сутры предлагают следующий рецепт: (Ekadhikena Purvena), что можно перевести как "на один больше, чем предыдущий". Из-за краткости сутр нельзя однозначно сказать, какая именно из операций - умножение или деление - имеется в виду: возможны оба варианта. Проиллюстрируем сказанное.
1. Метод деления "на один больше, чем предыдущий".
Разделим 1 на 19.
Последняя цифра делителя 9, предпоследняя 1; "на один больше, чем предыдущий"
= 1 + 1 = 2. Работает метод целочисленного деления на 2; остаток в каждом
пункте деления записывается спереди и снизу от соответствующей цифры частного.

(далее период начинает повторяться).
Приведем еще один пример. Разделим 1 на 29. <На один больше, чем 2> = 3, следовательно, будем выполнять деление на 3:

2. Метод умножения "на один больше, чем предыдущий".
Рассмотрим тот же пример 1/19; производится умножение на 2. Здесь используется тот факт, что частное от деления двух целых чисел есть бесконечная периодическая дробь. Последней цифрой периода частного является 1, поскольку делитель оканчивается на 9. Тем же способом производим последовательное умножение, но справа налево, записывая старший разряд снизу слева с последующим прибавлением.

Далее период начинает повторяться. Начало и конец периода обозначены точками сверху. Рассмотренные выше примеры дают оригинальный способ деления на числа, оканчивающиеся на 9, который не распространяется на случай произвольных целых чисел. Перейдем теперь к изложению регулярной процедуры. Рассмотренный алгоритм деления на числа, оканчивающиеся на 9, связан со свойствами умножения (следовательно, и деления) по модулю 10. (Умножение по модулю 10 означает отбрасывание в произведении целого числа степеней 10.) Напомним таблицу умножения на 9 (mod 10):
9 х 1 = 9 9 х 2 = 8 9 х 3 = 7 9 х 4 = 6 9 х 5 = 5 9 х 6 = 4 9 х 7 = 3 9 х 8 = 2 9 х 9 = 1
Как видим, сумма множителя и произведения равна 10. На этом же принципе основан специальный метод Никхилам. Соответствующая сутра (Nikhilam Navatascaramam Dasatah) читается так: "Все из 9, последнюю из 10". Данный метод, применяемый в обратную сторону, фактически уже рассматривался в главе об умножении. Так, при умножении 89х88 = 7832
89 - 11 88 - 12 _______ 77/1 32
последняя цифра дополнения получается вычитанием из 10 последней цифры
сомножителей: 10 - 9 = 1; 10 - 8 = 2; а первая цифра - вычитанием из 9
первой цифры сомножителей: 9 - 8 = 1. Эту же сутру используют и в некоторых
случаях деления. Перейдем к примерам.
Пример 1.
Рассмотрим деление двузначных чисел на 9 с получением частного и остатка:
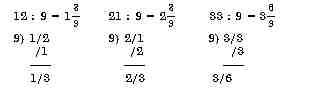
Здесь первую цифру делимого переносят вправо вниз на одну позицию и, складывая с последней цифрой, получают остаток. Само же частное совпадает с первой цифрой. Если делимое содержит большее число значащих цифр, являясь, например, двух- или трехзначным, то первую цифру делимого переносят на одну позицию вправо и вниз с последующим сложением с соответствующим разрядом делимого:
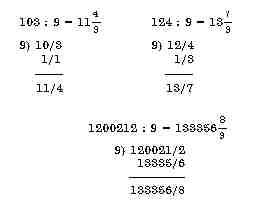
Если остаток превосходит делитель, то производят соответствующую операцию сложения.
Пример 2.

Аналогичные операции выполняют и при делении на 8, 7 и т. п.; остаток при этом однако домножают на дополнение до 10: на 2 для 8, на 3 для 7 и т. д.
Примеры.
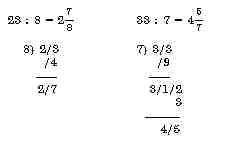
Таким образом, рассмотренный метод достаточно эффективен, если значащие цифры делимого незначительно отличаются от 9. Приведем еще два примера с большим числом значащих цифр.
